1. It would appear that a large portion of the inter-team variation in EV shooting percentage can be accounted for by random variation.
2. The spread among NHL teams is very slightly broader than what would be expected by chance alone. Therefore, it would appear that teams do in fact exert some influence on their EV shooting percentage.
* I actually only looked at 5-on-5 shooting percentage. I assume that the results are generalizable to even strength play as a whole, although that may not be the case.
In making my playoff predictions this year, I looked very closely at each team's shot rate (both SF and SA) in each of the main game situations (that is, 5-on-5, 5-on-4, 4-on-5). I also looked at how often each team had played in each game situation over the course the season. My method of determining the 'better' team basically revolved entirely around these two factors.
My method of evaluation didn't really accord much weight to the percentages, regardless of game state. I did this under the -- somewhat faulty -- assumption that most of the inter-team variation in the percentages is due to randomness. If true, there wouldn't be much point in taking the percentages into account when attempting to predict future results.
As it happens, that really isn't true at all. It appears to largely be true in terms of EV shooting percentage. However, this finding isn't necessarily generalizable to other game states. For one, it doesn't seem to be case for EV save percentage. More on that later.
It also doesn't seem to apply to 5-on-4 shooting percentage. While I began my analysis under the expectation that the majority of the inter-team variation in 5-on-4 shooting percentage could be explained through randomness, that doesn't appear to be true.
My methodology was basically identical to that used in my analysis of 5-on-5 shooting percentage, with one obvious difference -- instead of looking at 5-on-5 play, my focus this time was on 5-on-4 play. Here's a quick explanation of my method.
Firstly, I looked at how many shots each team took at 5-on-4 during the 2008-09 regular season. The values can be viewed at behindthenet. I then figured out the average 5-on-4 shooting percentage in the league (~0.128). I then simulated 100 'seasons'. In each 'season', the number of shots taken by each team was the number of 5-on-4 shots taken by that team during the 2008-09 season. However, the percentage of scoring a goal on each shot for every team was 0.128 -- the league average 5-on-4 shooting percentage. That is, each team was assigned the exact same shooting percentage. This is significant as, in any particular 'season', any deviation from the mean is strictly due to randomness, thus allowing one to determine how the spread in 5-on-4 should appear through the impact of randomness alone.
The results:
 The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.
The first graph is fairly straightforward. The blue distribution is the 'predicted' distribution. It represents the spread in 5-on-4 shooting percentage over the course of the 100 simulated seasons. Thus, it's an approximation of what the spread among teams in 5-on-4 shooting percentage would look like if each team had the exact same underlying 5-on4 shooting percentage.The red distribution is the 'actual' distribution. It represents the spread in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season. That mini-peak on the far right of the graph represents Philadelphia, who led the league with a gaudy 5-on-4 shooting percentage of 0.181.
 This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.
This graph is a 'smoothed' version of the above graph. The blue distribution required no smoothing and is therefore identical to the one above.However, the red distribution did require smoothing. Thus, the red distribution in this graph is simply a normal distribution with a mean of ~0.128 and standard deviation of 0.02. Why 0.02? That was the standard deviation in 5-on-4 shooting percentage among NHL teams during the 2008-09 season.
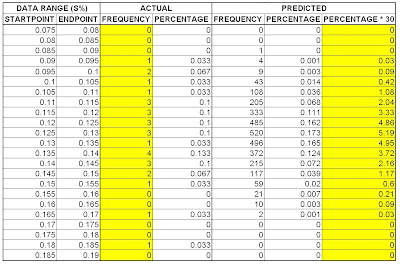 Here's the raw data. It's more or less self-explanatory.
Here's the raw data. It's more or less self-explanatory.The first two columns are the start and end points for the percentage 'ranges' (it's hard to make sense of non-discrete data). The 'actual' column -- the third one from the left -- shows the numerical distribution in 5-on-4 shooting percentage for the 2008-09 season. So, for example, one team in the NHL had a shooting percentage between 0.18 and 0.185 this season. The 4th column merely shows the relative frequency of the third column values.
In terms of the predicted values, the 5th column shows the frequency of each percentage range for the 100 simulated seasons, while the 6th column expresses those values as a relative frequency. So, for example, out of the 3000 simulated team-seasons (100 seasons * 30 teams = 3000 team-seasons), two teams had a shooting percentage falling between 0.165 and 0.170.
The final column merely shows the numerical distribution in shooting percentage in a hypothetical 30 team league where each team has the same underlying shooting percentage. This allows for a comparison to be made with the actual distribution, shown in the 3rd column.
 Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.
Finally, the supplemental data. For each of the 100 simulated seasons, I calculated the standard deviation in shooting percentage among the teams. 'PREDICTED ST DEV MEAN' is the average standard deviation over the 100 seasons. 'PREDICTED ST DEV MIN' is the minimum standard deviation for the 100 seasons. 'PREDICTED ST DEV MAX' is the maximum standard deviation for the 100 seasons. 'ACTUAL ST DEV' is the standard deviation in 5-on-4 shooting percentage among NHL teams for the 2008-09 regular season.The fact that the actual standard deviation is larger than the maximum standard deviation for any of the simulated seasons is fairly conclusive proof that randomness alone cannot account for the inter-team variation in 5-on-4 shooting percentage. For what it's worth, when I did my analysis on the effect of randomness on EV shooting percentage, some of the simulated seasons had a larger standard deviation than the actual standard deviation.
Lastly, the final row shows the inter-year correlation -- that is, for 0708 and 0809 -- in 5-on-4 shooting percentage at the team level. The value is non-trivially positive, which lends support to my above finding that teams can reliably influence their 5-on-4 shooting percentage.* Not surprisingly, the Flyers were tied for the league lead in 5-on-4 shooting percentage last season.
*On the other hand, Tyler at mc79hockey, in a post examining this type of thing at the start of the 2008-09 season, found an inter- year correlation that was somewhat lower, on the order of ~0.30.
EDIT:
Also relevant and of interest:
Vic Ferrari, in the comments section of this post -- in which he examines the ability of individuals player to effect PK SV% --, reports that individual Oilers had a substantial effect on powerplay shooting percentage while on the ice. This tends to support the idea that powerplay shooting percentage is highly non-random in its distribution.
14 comments:
Simply fascinating. To put it bluntly: I'm a fan!
Actually..my research shows the opposite to be true..that is to say that a teams power play success
is not repeatable to any statistically significant measure..wheras even strength goal scoring is ..Hav eyou looked at shooting % over 20 or 40 game segments..The key is to compare
correlations between a teams first 20 or 40 to there second 20 or 40
the stronger the correlation the more the stat is repeatable and thus the more the stat is likely determined by skill rather than luck. As I stated my research shows 5 on 5 is repeatable whereas special teams are not
Check advanced nfl stats.com and B. Burke's great site for more of the math behind tis approach
dan
"The key is to compare
correlations between a teams first 20 or 40 to there second 20 or 40
the stronger the correlation the more the stat is repeatable and thus the more the stat is likely determined by skill rather than luck."
I fail to see why this is "the key." Why is a sample of 20 to 40 games particularly significant? It seems like an arbitrary cutoff point to me. If a stat is particularly high in variance, it's still subject to the influence of skill, convergence might just take longer.
"a teams power play success
is not repeatable to any statistically significant measure."
Um, what? So you're saying that Philly, Detroit and Washington finishing 2nd,3rd, and 4th last season and then 1st,2nd, and 3rd this season in PP scoring is simply a total fluke?
What am I missing?
Dan:
I'm not sure which data you've looked at, but there is in fact a statistically significant correlation between team powerplay performance at Time 1 and team powerplay performance at Time 2.
I suspect that you've looked at an insufficiently large sample of games when analyzing the data.
Sunny is correct in that the relationship does take some time to materialize, and can therefore only be discerned if the sample of games is sufficiently large.
For example, here are the inter-year correlations in power play conversion rate at the team level. Powerplay conversion rate may not be a perfect measure of powerplay performance, but it's good enough.
YEAR1-YEAR2-----r
=====================
0607-0708 ------ 0.407
0506-0607 ------ 0.32
0304-0506 ------ 0.455
0203-0304 ------ 0.315
0102-0203 ------ 0.496
0001-0102 ------ 0.474
9900-0001 ------ 0.376
9798-9899 ------ 0.025
I'm not sure if all of those values are statistically significant -- the last one certainly isn't. However, looking at the values as a whole, it's fairly clear that powerplay conversion rate in year n is positively correlated with powerplay conversion rate in year n+1.
Jlikens;
To start are you able to verify my claim that ther is a low correlation between first half power play rate and second half power play rate?
thanks perhaps my research is flawed?
However, If this is true what does it mean?
My claim is simply that if pp % is a repeatable skill a team should be able to repeat their pp% from the first 1/2 to the second half..This seems reasonable to me ..its 1/2 a season!!!
Jlikens;
thanks for your research!!
If my data is correct than this year is similiar to 97-98.
What is your interpretaion of a year like this?
I am not sure what the interpretation means for these to years? Why should these two years
differ?
But I contend that 1/2 a season MUST be a large enough sample.
Year to year is problematic due to the increased change in rosters etc.
Ceraldi,
You are way WAY off in what constitutes a reasonable sample with regards to goal scoring rates. You're not alone - many people are simply unaware of just how much randomness there is in the NHL when it comes to scoring, and just how long it takes for noise to smooth out. One full season is really not even a big enough sample size when it comes to measuring certain statistics.
Half a season's worth of PP shots is like 200 shots. LOL. Even 2000 shots would still have a good amount of error with regards to save/shooting % (and therefore, number of goals for and goals against). For example, Chris from hockeynumbers once wrote "one thing people often forget about save percentages is the amount of error is significant, even for goaltenders who play a lot, for example a goaltender who faces 500 shots has approximately 2.5% error, or has a save percentage of 0.908 ± 0.025 or it has a 95% confidence interval of (.934, 882), Luongo with approximately 2500 shots is (.925, .903), which in terms of quality is a huge difference, in fact that range covers the top 20 goaltenders of 2005-2006."
This is why a lot of us around here use stats like Corsi or Expected Goals, because when dealing with small sample sizes they're often much more predictive of future production.
JLikens,
Wouldn't the fact that shooting percentages are a good bit higher on the PP than ES mean that there will be less variance?
Dan/Mr.Ceraldi:
"To start are you able to verify my claim that ther is a low correlation between first half power play rate and second half power play rate?
thanks perhaps my research is flawed?
However, If this is true what does it mean?
My claim is simply that if pp % is a repeatable skill a team should be able to repeat their pp% from the first 1/2 to the second half..This seems reasonable to me ..its 1/2 a season!!!"
The problem with looking at the intra-season split half reliability for power play performance is that the relevant data simply isn't readily available.
On the other hand, NHL.com contains basic powerplay statistics for every team going back to the 1997-98 season. Thus, it's much easier to look at the interyear correlation.
I'll agree with you that, at least in theory, comparing first half performance to second half performance is the superior method.
The only year that I have such data on is the 2008-09 season. The advanced power play statistics are from at about the ~48 game mark of the season. Obviously, this is a tad past the midway point of the season, but it still allows for a comparison to be made between team powerplay performance up to that point and subsequent powerplay performance over the remainder of the regular season. Here are the correlations:
METRIC ----------------- r
==============================
PP Goals For/60 -------- 0.822
Shots For/60 -------- 0.851
PP Shooting PCT -------- 0.777
So, at least for 2008-09, powerplay performance in the first half of the season is strongly predictive of powerplay performance in the second half of the season.
"thanks for your research!!
If my data is correct than this year is similiar to 97-98.
What is your interpretaion of a year like this?
I am not sure what the interpretation means for these to years? Why should these two years
differ?".
I'm not sure how to account for the lack of correlation between power play conversion rate in 1997-98 and power play conversion rate in 1998-99. It looks as though both Anaheim and St.Louis had two of the worst powerplays in the league in 1997-98, yet two of the strongest powerplays in the following season. That might have something to do with it.
Sunny:
"Wouldn't the fact that shooting percentages are a good bit higher on the PP than ES mean that there will be less variance?"In the sense that a higher shooting percentage leads to higher frequency of goals?
Hmmm...
I'm not sure if that would be the case, theoretically speaking.
As it happens, there is actually more variance among NHL teams in PP S% than in EV S%, which can be accounted for by two reasons:
1. The fact that, over the course of an NHL season, there are many more shots taken at EV then on the power play. The greater the number of shots, the less randomness contributes to inter-team variation in shooting percentage (in an absolute sense).
2. The fact that the PP S% has a greater 'team-skill' component than EV S% -- that is, the contribution of random variation to PP S% is relatively weaker.
So, if the fact that PP S% is higher than EV S% does tend to reduce variance, this effect is counterbalanced by the above factors.
Good stuff as always.
It's tough to say with the actual distribution being discrete and with only 30 samples. Just off the top of my head, but I think you would need a larger sample (maybe 50 games randomly selected from each team's schedule over and over again) to get the observed distribution clear in form.
Then you could hypothesize a beta distribution as the distribution of ability, take a starting guess at the exponent multiplier at 300 or so to start, then parlay it through with Bernoulli trials, you new ability distribution through the binomial(ish) prior you created above. And see how well it works.
Then keep adjusting the ability distribution constants until you get a best fit, then abandon the beta entirely and just try to build a curve out of splines that works best.
That done, you would have a hell of a model.
Does that make sense? I may well be wrong, just spitballing.
BTW:
This url:
http://www.timeonice.com/gamePPinfo0708.php?gamenumber=20747
gets you the 5v4 PP info on a game by game basis.
If you wrote a calling script you could scrape off all 1230 games from 0708. Because some random selections of 41 games will have a much higher correlation to the other 41 games than others will, just by chance alone. I usually just use season splits as well, just to save time, but when I'm feeling more ambitious this is clearly the better way to go.
"It's tough to say with the actual distribution being discrete and with only 30 samples. Just off the top of my head, but I think you would need a larger sample (maybe 50 games randomly selected from each team's schedule over and over again) to get the observed distribution clear in form."Yeah, that's a good point. The limited number of samples is definitely a problem.
And while using a normal curve with the same mean and standard deviation smoothes out the data, it presumes that the true variance is equivalent to the observed variance, which may or may not be the case.
Just looking at the 07-08 data from behindthenet, for example, it seems that the standard deviation in PP S% was lower than it was for this year. So perhaps 08-09 was a bit anomalous, leading me to overstate the 'team' contribution to PP S%.
I take it that you've looked at this type of thing before. What's your take on PP S%? I know that you mentioned in one of your posts that individual players were able to influence their on-ice PP S%.
"Then you could hypothesize a beta distribution as the distribution of ability, take a starting guess at the exponent multiplier at 300 or so to start, then parlay it through with Bernoulli trials, you new ability distribution through the binomial(ish) prior you created above. And see how well it works.
Then keep adjusting the ability distribution constants until you get a best fit, then abandon the beta entirely and just try to build a curve out of splines that works best.
That done, you would have a hell of a model.
Does that make sense? I may well be wrong, just spitballing."Heh. I think that you've lost me here.
BTW:
This url:
http://www.timeonice.com/gamePPinfo0708.php?gamenumber=20747
gets you the 5v4 PP info on a game by game basis.
If you wrote a calling script you could scrape off all 1230 games from 0708. Because some random selections of 41 games will have a much higher correlation to the other 41 games than others will, just by chance alone. I usually just use season splits as well, just to save time, but when I'm feeling more ambitious this is clearly the better way to go.Thanks for the link.
Yeah, that would be the better method.
Unfortunately, my programming skills are, well, non-existent.
Yeah, intuitively 08/09 does seem a bit anomalous, but it's still a huge factor.
IIRC then home teams tend to shoot a bit more (home fans should feel reassured that their relentless cries of Shooooooot! are being listened to, at least a bit. But their shooting% drops a commensurate amount, if that makes sense.
PPs are tricky. I think that rolling averages would reveal a lot. Meaning I think that when teams go through stretches of being selective with their shots, the shooting percentage goes up ... and when they go through stretches of just shooting it on net, the shooting percetage goes down.
Special teams in hockey are like baseball ... it seems simpler than 5v5 hockey but it isn't. Players have to much time to think, offense and defense become divorced, it gets tricky. And I sure as hell don't have the answers.
Post a Comment